YANMAR Technical Review

Abstract

Elastoplastic analysis under cyclic loadings is increasingly required in recent years. There are several models to describe elastoplastic behavior. Among them, the extended subloading surface model is able to express smooth transition from elastic to plastic state that is observed in real metal. And the extended subloading surface model is one of the most competent models for describing cyclic loading behavior. In order to use the extended subloading surface model under finite element software, it is necessary to apply the implicit stress-update algorithm by return-mapping and the consistent tangent modulus tensor. They are implemented into the implicit finite element program through the user-defined function. We simulate elastoplastic behavior of cast iron material assess calculation accuracy and efficiency of the proposed algorithm.

1. Introduction

Use of CAE in industry has grown rapidly over recent years, with strength analysis being one application of particular importance. One example of where strength analysis is used to improve design quality is the need to ensure reliability with respect to thermal fatigue failure, whereby cracks form in cylinder heads, pistons, or other parts due to the thermal load during engine starting and stopping. Achieving this requires the highly accurate reproduction of elastoplastic behavior, including under cyclic loads. The extended subloading surface model^{(1, 2)} adopted for this research is able to express elastoplastic behavior in which there is a smooth transition from elastic to plastic deformation. This makes it suitable for reproducing the elastoplastic behavior of materials like the cast iron widely used for engine components that has a narrow range of pure elastic behavior and a smooth transition to plastic deformation. Moreover, among the various elastoplastic models that have been proposed^(3-5), the extended subloading surface model has been proved to be one that can accurately reproduce cyclic elastoplastic behavior⁽¹⁾．

To introduce the extended subloading surface model into a static FEM analysis, the research described here applied it to an implicit stress-update algorithm by return-mapping and the consistent tangent modulus tensor⁽²⁾. This was implemented by utilizing the user-defined function of ADVENTURECluster, a general-purpose FEM program, establishing an analysis technique that can perform stable and efficient calculations on structures such as engines. The technique was then utilized to reproduce the elastoplastic behavior of cast iron and its effectiveness was verified through comparison with the Chaboche model⁽³⁾ widely used in commercial FEM software.

2. Formulation

2.1. Formulation of Extended Subloading Surface Model

This section summarizes the basic equations which are used in the extended subloading surface model described in this article⁽¹⁾．The infinitesimal theory based on the small strain is adopted. The strain 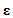is expressed as the sum of the elastic strain 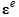and plastic strain 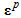(equation (1)). The Cauchy stress 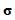in the elastoplastic state is expressed by equation (2) using the isotropic linear Hooke's law with elastic modulus tensor .

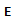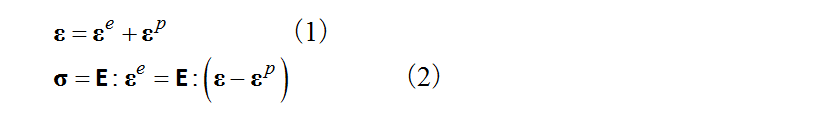
A normal yield surface 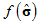expressed by equation (3) which contains isotropic hardening and kinematic hardening and a subloading surface 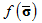expressed by equation (4) which is similar to the normal yield surface and passes through the current stress point are assumed (see Fig. 1). Equation (5) gives the various physical quantities for the subloading surface.

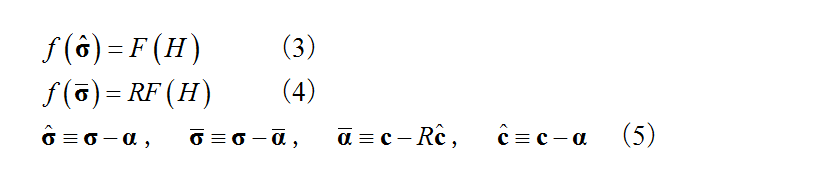
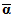is the center of the subloading surface, being the conjugate point on the subloading surface correspond to the back stress 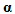. 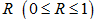is the normal yield ratio, and the subloading surface coincides with the normal yield surface when 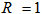. A related flow rule using the outward normal vector 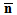for the subloading surface and the plastic multiplier 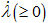which are expressed by equation (6) is adopted for the plastic strain increment.

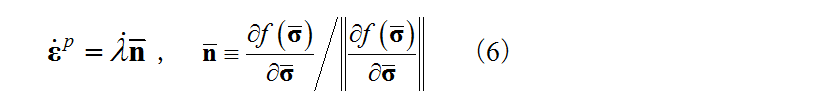
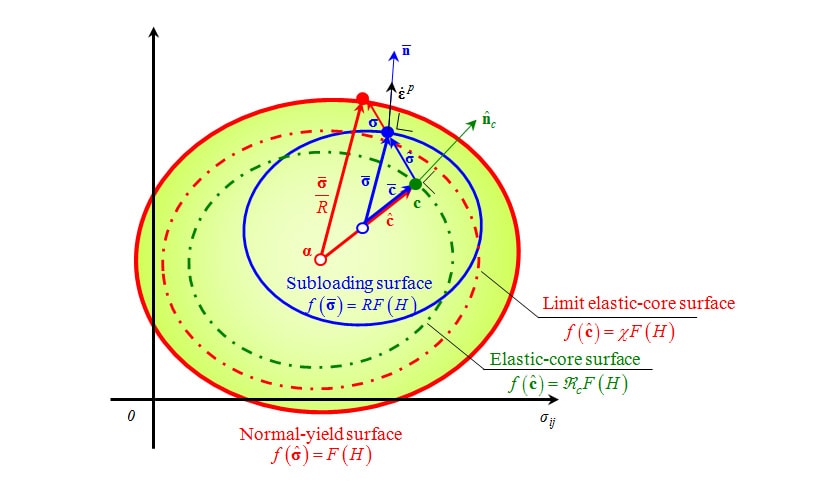
Equations (7) and (8) give the evolution rule for the normal yield ratio, which integrate to give equation (9). Note that 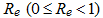is a material constant that expresses the normal yield ratio at the pure elastic limit, and the current stress point is in the elastic state as long as it is within the pure elastic limit.

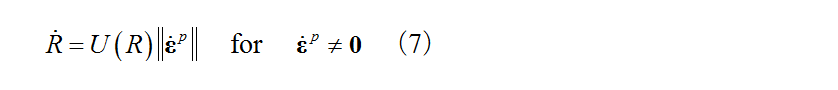
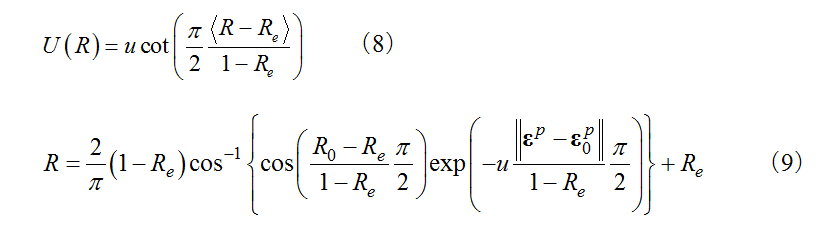
The non-linear equations (10) to (12), which are evolving with the increase in accumulated equivalent plastic strain, are adopted for the isotropic hardening function 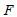, kinematic hardening 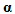, and similarity center .

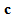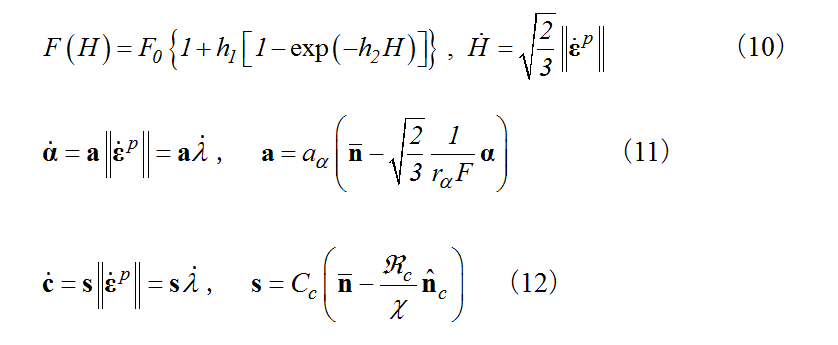
Here, 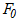is the initial value of the normal-yield surface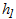, 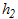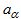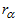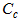and ，，，，, and 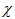are material constants.

2.2. Implicit Stress-update Algorithm

Fig. 2 shows the overall flowchart for the stress-update algorithm using return-mapping. The calculation in step 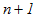is performed by adding the strain increment 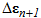to the stress 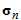, elastic strain 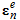, and other state variables updated in step 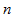. Return-mapping calculates the trial elastic stress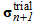， based on the assumption that the whole strain increment is elastic strain (equation (13)). Next, whether or not yield has occurred is determined from this calculated trial elastic stress 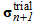on the basis of equation (14). Here, the subscript indicates the number of steps.

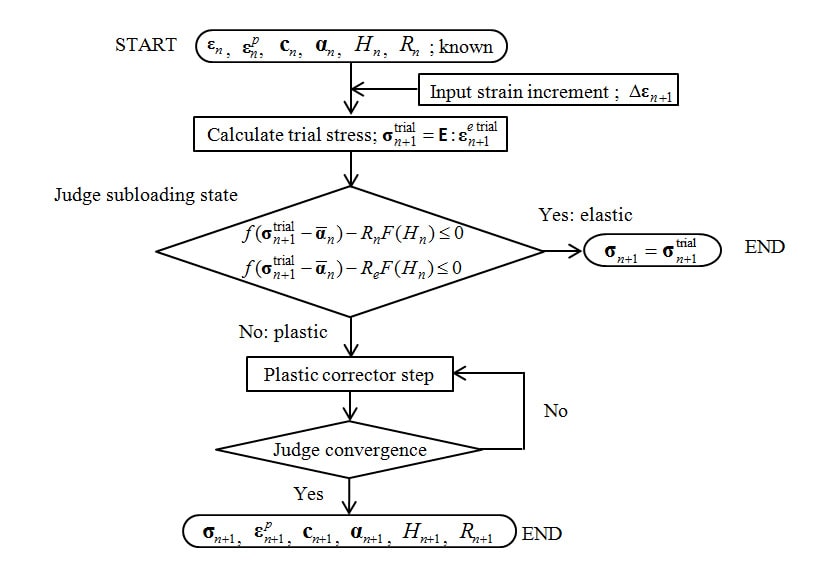
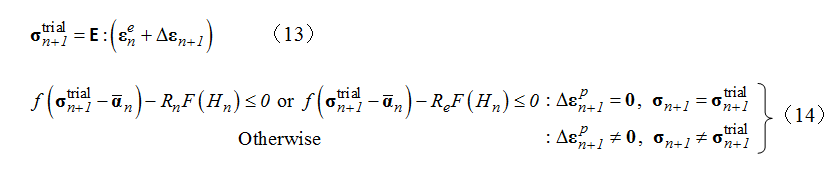
As the upper condition of equation (14) corresponds to the case when the material has not yielded (elastic deformation only), the trial elastic stress is used as the new value and stress updating is complete. In contrast, the lower condition corresponds to when yield has occurred and in this case plastic correction is performed.

Plastic correction applies the Newton-Rapson method to the yield surface obtained from the trial elastic stress in return-mapping to calculate the stress and state variables after plastic deformation by iteratively converging the stress on the subloading surface. To achieve this, the initial values of the stress and state variables for the iterative calculation are first formulated as indicated by equation (15). Here, the superscript indicates the number of iterations of the convergence calculation.

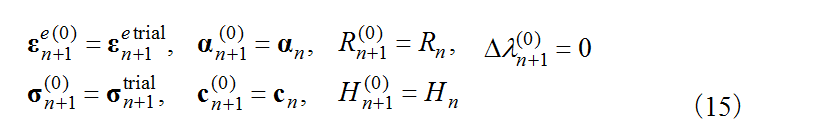
Equation (16) expresses the equilibrium condition that must be satisfied, including the stress, subloading surface equation, and state variables. The unknown vector 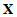and the residual vector 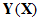are given in equations (17) and (18) respectively, and the equilibrium equation to solve is given in equation (19).

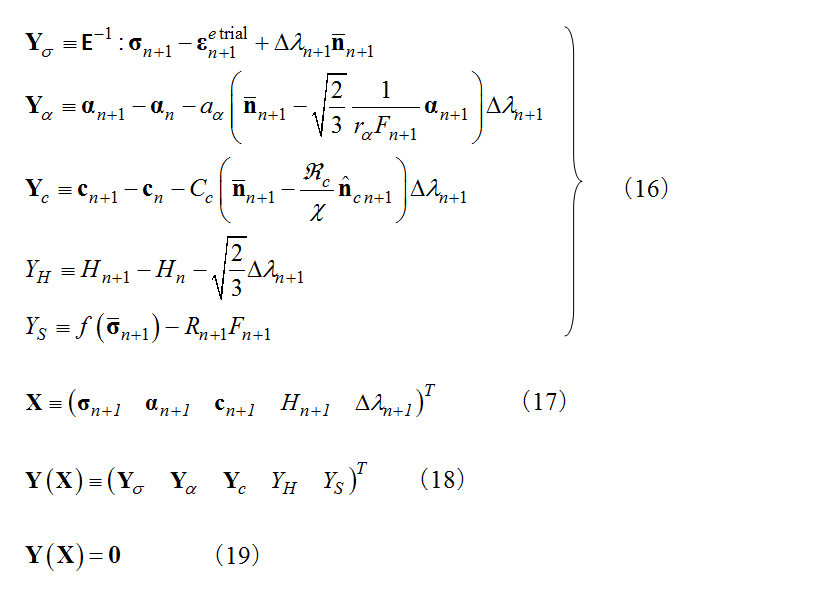
Equation (19) is a non-linear simultaneous equation. To solve it by an iterative calculation using the Newton-Raphson method, it is linearized by a Taylor expansion to give equation (20).

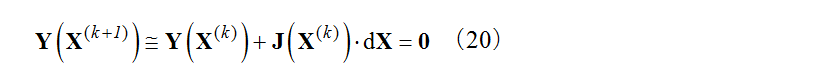
The Jacobian matrix 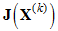in the above equation (20) is given by equation (21).

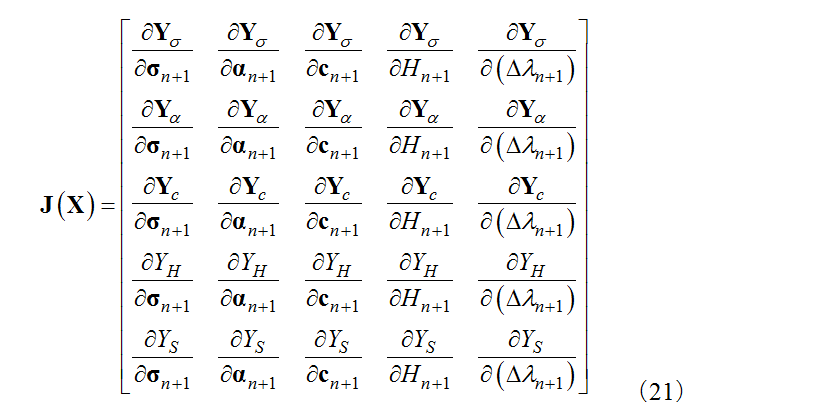
The Jacobian matrix is made up of the second order tensor 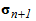, and 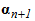, 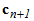and the scalar quantities 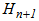and 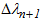. While calculation of each element of the Jacobian matrix is complex, they can be obtained by direct differentiation and therefore the detail is omitted here. Equation (22) is used to calculate the correction vector 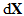for the iteration 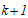from the iteration 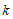of the convergence calculation, and this equation (22) is used to update the unknown vector 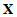as shown in equation (23). The convergence calculation continues until it satisfies the criterion in equation (24), and the converged values of the stress and state variables are used as the new values after the plastic correction.

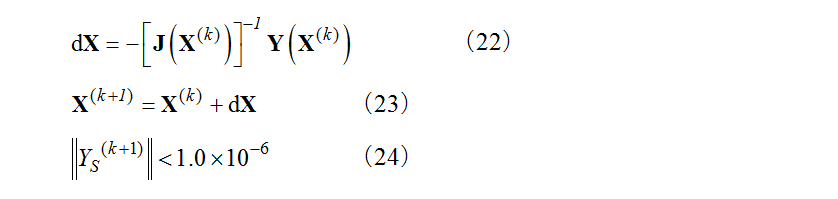
For a consistent tangent modulus tensor that efficiently satisfies the global equilibrium condition in the static FEM model, it is necessary to consider perturbations in the stress and strain at the point when stress updating is complete for step . Accordingly, the parts that relate to stress updating are calculated from the inverse of the Jacobian matrix and used in the global calculation as the consistent tangent modulus tensor.

A numerical analysis was performed in which the above algorithm was incorporated into ADVENTURECluster by using its user-defined function.

3. Analysis Results

3.1. Verification of Implicit Stress-update Algorithm Suitability

To verify that the implicit stress-update algorithm is suitable for practical deformation analyses, a cyclic deformation analysis was performed for the cylindrical test specimen shown in Fig. 3, which includes a round notch. The analysis used a 1/2 model (taking advantage of axial symmetry) and a mesh made up of hexahedron first-order elements. Two types of cyclic deformation analysis were performed in which the boundary conditions were a displacement constraint on the bottom surface in the axial and circumferential directions, and forcible displacement of the top surface in accordance with the conditions specified below.

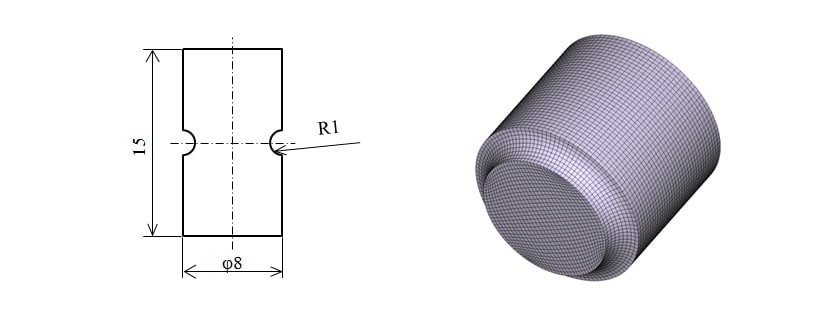
Condition Ⅰ
Cyclic tensile and compressive deformation in the axial direction, with a displacement amplitude of ±0.05 mm and a displacement increment of 0.01 mm.

Condition Ⅱ
Cyclic torsional deformation in the circumferential direction, with a torsional amplitude of ±2 degrees and an increment of 2/5 degree

The analysis continued for five cycles of each type of deformation, a total of 95 steps. The convergence criterion of the global calculation was that the absolute value of the largest element of the residual force vector be 1.0×10^-4 N or less.

Fig. 4 a) shows the Mises equivalent stress distribution after the first cycle under the condition I at a forcible displacement of 0.05 mm, and Fig. 4 b) shows the result after the last cycle. The stress in the cylindrical test specimen with a round notch increased with each cycle. The stress concentration at the notched section was found due to the notch effect. Fig. 4 c) shows the Mises equivalent stress distribution after the last cycle under the condition II. The stress concentration at the notched section was seen as well as the case of condition I. These results indicate that the proposed return-mapping method provides a valid analysis for cyclic deformations with both tension/compression and torsion.

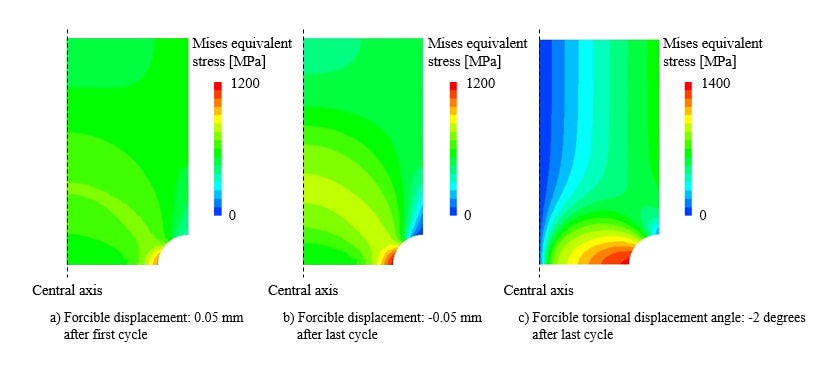
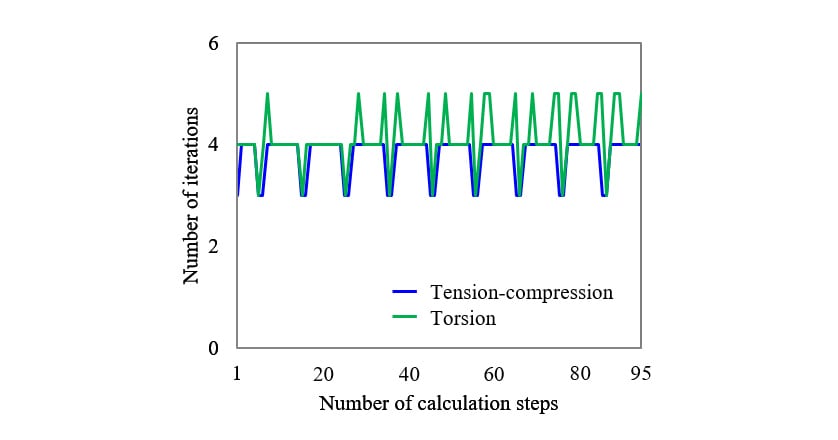
Fig. 5 shows the number of iterations required for convergence in the global calculation of each step. The global calculation used in this method converges with a maximum of five iterations in the case of condition II, which is hard to converge. Fig. 6 shows the degree of convergence of the residual force vector after the last step in a cycle for both analyses. The proposed method achieved quadratic convergence of the largest element of the residual vector in both analyses, indicating that it has good convergence performance by the introduction of the consistent tangent modulus tensor.

3.2. Comparison of Calculation and Experiment for Cast Iron

The accuracy with which the extended subloading surface model reproduces elastoplastic behavior was verified using stress-strain curves obtained by experimental testing of cast iron. The test specimen was made of FCD450 spheroidal graphite cast iron. The stress and strain were measured by applying an amplitude of 0.5% strain (nominal strain) for 100 cycles.

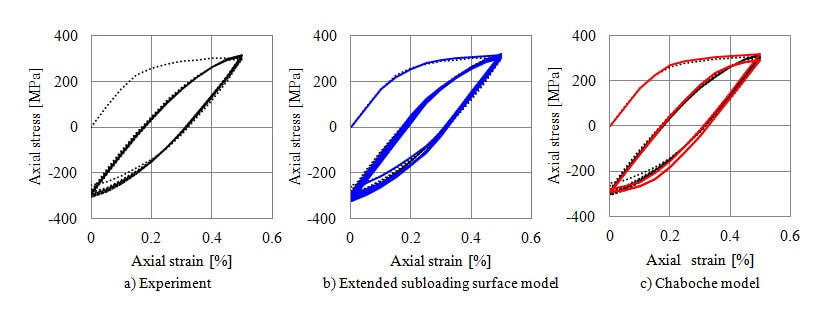
To verify the accuracy with which the analysis reproduces stress and strain, calculations were performed using Chaboche model in addition to the extended subloading surface model. The analysis used a strain increment of 0.05% and hexahedron first-order elements for the model which are the simplest. Fig. 7 shows the comparison of the measured and calculated stress and strain after 1, 10, 20, 30, 40, 50, 60, 70, 80, 90, and 100 cycles. Compared to the Chaboche model, the extended subloading surface model achieves good agreement with the stress and strain across all cycles. In particular, the extended subloading surface model accurately reproduces the stress and strain when load is reapplied after unloading from a yield condition due to movement of the similarity center. This indicates that analyses using the extended subloading surface model can reproduce the elastoplastic behavior of cast iron with high accuracy.

4. Conclusions

The work described in this article involved the development of a highly accurate elastoplastic analysis technique by implementing the extended subloading surface model in ADVENTURECluster, a general-purpose FEM program. This resulted in the following conclusions.

• A stable and efficient calculation can be achieved by applying the extended subloading surface model to consistent tangent modulus tensor and an implicit stress-update algorithm by using a return-mapping.
• The extended subloading surface model has been proved to provide highly accurate predictions of cyclic stress-strain behavior in cast iron.

Although not included in this article, the technique is being used to predict the thermal fatigue life of cylinder heads, pistons, and other engine parts. The aim for the future is to contribute to reducing product costs by expanding targets and improving reliability through further improvements in accuracy made by taking account of other material behaviors, including high-temperature creep and temperature-dependency.

5. References

• (1)Hashiguchi, K., Elastoplasticity Theory (2013), Springer.
• (2)Anjiki, T., Oka, M, and Hashiguchi, K., Elastoplastic analysis by complete implicit stress-update algorithm based on the extended subloading surface model, Transactions of the JSME, Vol.82, No.839 (2016), DOI:10.1299/transjsme.16-00029.
• (3)Chaboche, J. L., Time-independent constitutive theories for cyclic plasticity, International Journal of Plasticity, Vol.2, No.2 (1986), pp.149-188.
• (4)Dafalias, Y. F. and Popov, E. P., A model of nonlinearly hardening materials for complex loading, Acta Mechanica, Vol.21 (1975), pp.173-192.
• (5)Mroz, Z., On the description of anisotropic workhardening, Journal of the Mechanics and Physics of Solids, Vol.15 (1967), pp.163-175.

-IMPORTANT-

The original technical report is written in Japanese.

This document was translated by Research & Development Management Division.