ヤンマーテクニカルレビュー

Abstract

Robotics technologies such as automation for agriculture field are needed to promote labor-saving. One of the most relevant problems in automated agriculture is represented by controlling the robot along a predetermined path in presence of rough terrain or incline ground. In agricultural field, disturbances originating from interaction with the ground, such as slipping, make it quite difficult to achieve the required accuracy. In general, it is required to move within about 5 cm accuracy with respect to the predetermined path. Moreover, lateral velocity caused by gravity on the incline field also affects slipping. In this technical review, a path-tracking controller for agricultural tracked vehicles moving on rough terrains of incline field is introduced. The effectiveness of the proposed controller is tested in a simulation environment.

1. Introduction

With rises in global population comes the problem of food shortages. For instance, in Japan the number of farmers is decreasing, while their average age is rapidly increasing [1]. For these reasons, automation technologies such as autonomous driving are needed to work large fields with fewer farmers. On the other hand, environmental problems such as soil structure damage have been identified due to the increasing size of agricultural machines, especially in northern Europe. To this regard, small- sized tracked machines could represent a promising solution since larger contact area and lower contact pressure between the tracks and the ground would ensure at the same time better motion performance and lower pressure on soil [2], [3]. Therefore, small-sized tracked mobile robots will likely spread in the agricultural market in the next few years.

One of the most relevant problems in automated agriculture is represented by controlling a machine along a predetermined path in presence of rough terrain or inclined ground. Furthermore, the presence of ridges requires agriculture vehicles to move within about 5 cm accuracy with respect to the predetermined path. Unfortunately, the effect of gravity on inclined fields may generate slipping phenomena, thus making it quite difficult for the robot to achieve the required accuracy. Moreover, slipping depends on soil conditions, which in turn depend on geographical location, climate and other environmental factors, that cannot be modelled in a simple and accurate way. In order to address these shortcomings, techniques based on disturbance observation have been recently proposed [5], [6]. The disturbance observer (DOB) basically consists of an inner-loop controller, whose primary role is to compensate uncertainly in the plant and to reject exogenous process disturbances, thus making the inner-loop behave-like the nominal plant model.

We introduce our technical approach about autonomous driving controller for tracked agricultural vehicle in this technical review. The main contribution of our approach consists of the design of a control algorithm for tracked vehicles. This algorithm ensures path-tracking capabilities while moving in presence of slip phenomena that are due to either rough terrain and/or ground inclination. At first, slipping rejection is realized by using the DOB to adapt the target velocities (linear and angular) computed by the tracking controller. Unfortunately, this solution does not perform very well on inclined fields, since in these scenarios slipping is mainly due to the lateral velocity caused by gravity. Nevertheless, whenever the robot slips, its linear velocity and turning radius change. Virtually, this situation is equivalent to considering the instantaneous centers of rotation (ICRs) as time-varying parameters, rather than fixed quantities. Consequently, slip rejection can be achieved by integrating a parametric kinematic model of the robot inside the control algorithm, thus allowing to define virtual ICRs and to compensate slipping by adapting the virtual kinematic parameter. As a result, the main advantages of this approach consist in eliminating the need to: (i) either measure or estimate the dynamic parameters of the system; (ii) re-tune control gains whenever soil conditions change.

2. Path-Tracking Control Algorithm

2.1. Kinematic Model of the Vehicle

Fig. 1 shows the kinematic model of the tracked vehicle, where is the vehicle’s tread, is the robot orientation with respect to the Cartesian Frame x-y, 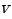is the vehicle linear velocity and 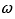is the vehicle angular velocity.

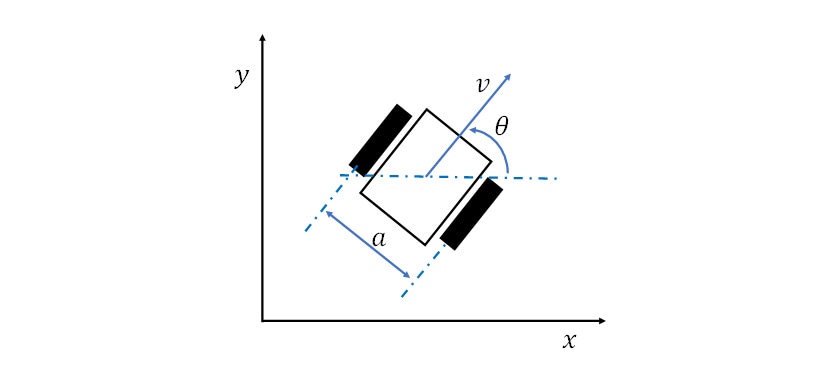
We consider a typical differential drive robot, whose kinematics can be modelled as follows [7]:

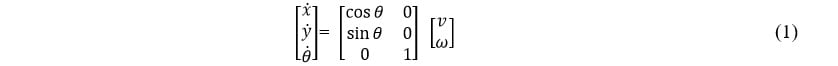
It is worth noticing that this kinematic model does not take into account slipping and skidding.

2.2. Path Tracking Control

First, let us define the path-tracking problem as the need to control linear and angular velocities in such a way that the robot follows a reference path at a desired speed. The reference robot model is the following:

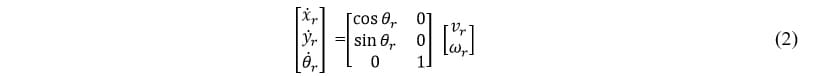
where 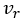is the reference linear velocity, and 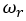is the reference angular velocity. We assume that 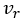and 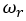, as well as their derivatives, are bounded. Moreover, we suppose that they do not tend to zero simultaneously. Given these hypothesis, we can define the equivalent trajectory tracking errors as:

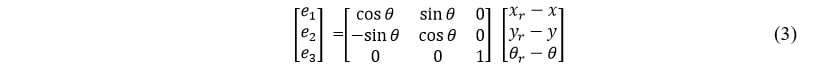
According to [8], the following function

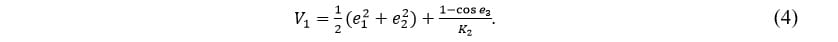
is a valid Lyapunov function, provided that target velocities are set as follows:

where 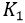, 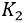and are control gains. Please notice that, at this stage, the control law ensures the convergence to zero of the errors, but it does not take into account slipping. To compensate this phenomenon, we implement the DOB for both linear and angular velocity, as shown in Fig. 2. For the sake of clarity, the block labelled as “Tracking Control” refers to (5). We also consider the location of the ICRs as an unknown parameter that is estimated by the “Adaptive Control” block ( ) and sent as input to the Angular velocity DOB.

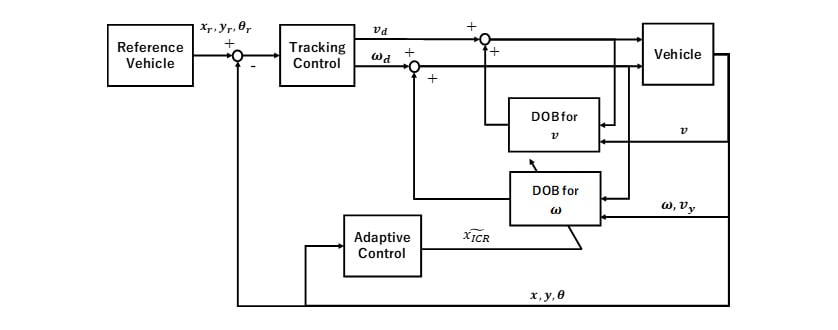
2.3. Disturbance Observer

Let us consider the side slipping due to lateral velocity caused by gravity on the incline field. According to [4], [9], we can re-write the robot kinematics model including the lateral velocity as follows:

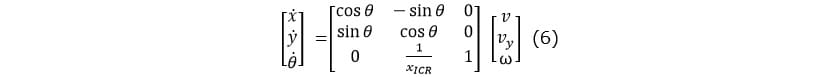
where 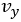is lateral velocity, and 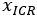is the ICR location on the longitudinal direction. We assume that both 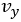and its derivative are bounded and we define the nominal model of the Angular velocity DOB according to equation (6). Then, we consider the location of the ICR as an unknown parameter, thus using as input the virtual ICR location ( ) estimated by the adaptive controller. Finally, we define 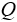as the low-pass filter. As a result, we obtain the Angular velocity DOB shown in Fig.3.

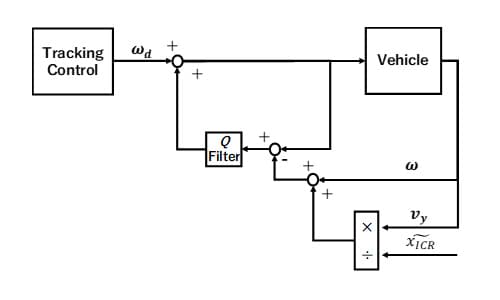
Fig. 3 Block diagram of DOB about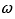

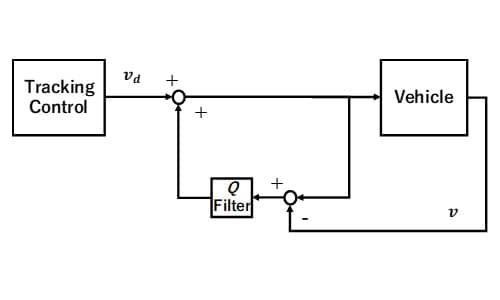
Fig. 4 Block diagram of DOB about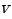

Moving to the linear velocity, the nominal model is simply equal to “1”, as it is shown Fig. 4. Given their structure, the two DOBs are able to compensate slip phenomena, thus guaranteeing that the system behaves as its nominal model [10].

2.4. Adaptive Control

In the previous section, we re-defined the angular velocity according to equation (6). Let us consider the Lyapunov function (4) again and let us compute the derivatives of equation (3), by substituting equations (5) and (6):

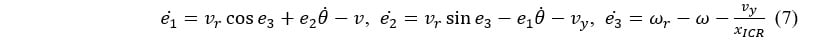
Then, the derivative of equation (4) can be computed as:

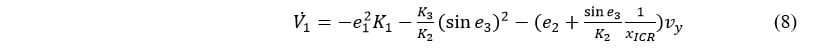
Now, let us introduce another Lyapunov candidate function, named :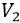

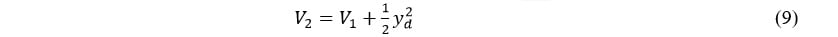
where 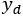is the vehicle lateral displacement generated by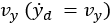. Since the tracked vehicle cannot move along this direction, 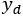necessarily represents the lateral deviation caused by side slipping. By differentiating equation (9), we obtain:

If we define the estimate of the virtual ICR location as follows:

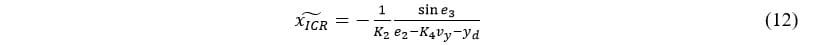
where 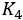is a positive control gain, we get:

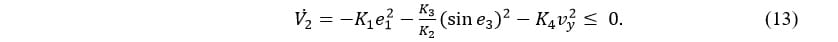
Since 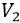is bounded from below and (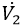) is negative semi-definite, 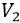converge to a finite limit. As a consequence, 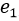, , 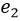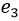and 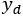are all bounded. Moreover, by considering equations (7) and (13), the second derivative of 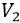can be written as

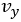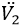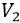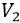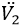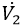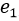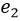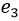From the above results, and since and its derivative are bounded, we can state that also is bounded. Given the fact that: (i) is continuously differentiable respect to time, (ii) converges to some constant value, (iii) is bounded, by Barbalat’s lemma, → 0 as t → [11], [12]. As a result, ,, and 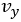converge to zero (Further details regarding the proof can be found in [16]).

3. Simulaton Results

3.1. Simulation Model

The experimental platform used to test our controller is the Xbot, an electrically driven tracked mobile robot manufactured by Dronyx [13]. Fig. 5 shows the Xbot and its simulation model develop using V-Rep simulation environment [14].

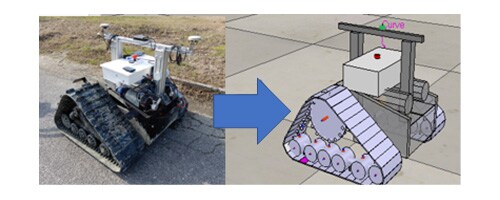
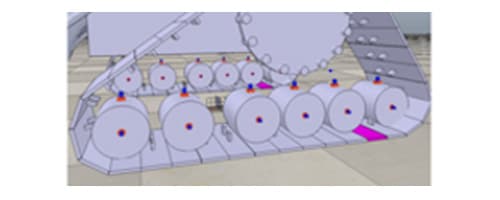
In order to simulate the motion of the tracks, we use a wheel-based model, as it is shown in Fig. 6. The system contains 6 rollers per side that are in contact with the ground surface. The vehicle is able to move thanks to the friction force generated by each wheel. The friction force is computed by the Vortex physical engine developed by CM Labs [15]. Further details regarding the simulation models of the tracks can be found in [17].

3.2. Simulation Results

A first simulation is performed by making the robot climb along a straight reference path on the incline field. We set the incline angle to 10 degrees. In order to simulate slipping phenomena (due for instance to the presence of mud) we reduce the target speed of the right track by 20% in the interval between 10 and 13 seconds from the simulation start. We refer to the Lyapunov-based control law (5) as “Conventional controller”, while we refer to our proposed controller as “Adaptive DOB”. We set the target speed as 0.5 m/s, and controller gains as (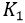,,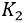,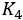)=(1.2,1.8,2.0,0.5) for both controllers. Finally, the cut off frequency of the low pass filter inside to DOB is set to 2 Hz. Fig. 9 shows how the two controllers are able to track the straight reference path, but it also demonstrates the superior performance of the Adaptive DOB in terms of reduce lateral deviation from the reference path.

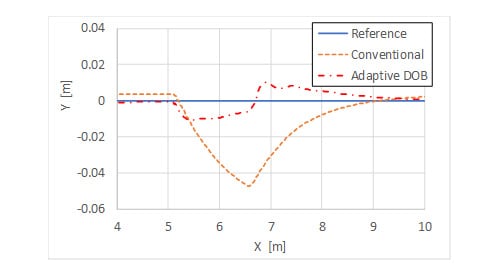
More in depth, Fig. 10 shows the lateral error, i.e. the tracking error in equation (3). Before the robot starts slipping (i.e. prior to 10 sec) the two controllers entail similar performance. As soon as the robot starts slipping, the Conventional controller is not able to reject the disturbance effectively and the lateral error significantly increase. On the other hand, the Adaptive DOB is able to reject the slipping and to limit the lateral error.

Fig. 11 shows the results of a different simulations during which the robot follows a typical vineyard-like trajectory. More in depth, the robot starts by climbing along the field, it performs a 180 degrees turn, it descends the field, it makes another 180 degrees turn, and, finally, it climbs along the field once again. The vehicle speed is 0.5 m/s, and the controllers are tuned with the previously displayed gains. Differently from the previous scenario, in this case a third control algorithm was considered in addition to the Conventional controller and the Adaptive DOB. This third controller is labelled as “Normal DOB” and it consists in a version of the DOB that relies only on kinematic model (1), without taking into account nor lateral velocity, neither adaptive parameters.

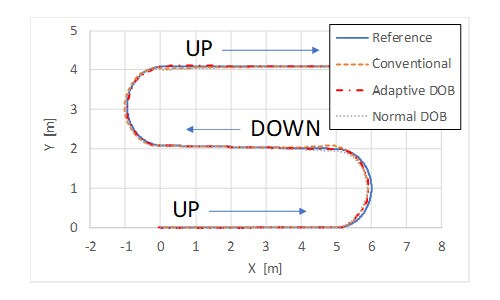
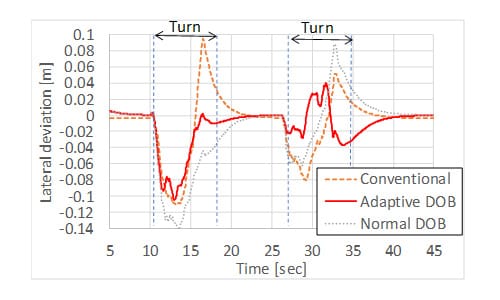
Fig. 12 demonstrate that the Adaptive DOB entails better performance in terms of reduced lateral error with respect to the Conventional one. Moreover, the comparison between the Adaptive DOB and the Normal DOB shows that the convergence of the error to zero is much faster when considering the adaptive kinematic model, thus proving that the adaptive controller is able to better counteract the effect of the lateral velocity caused by gravity. We also compared the performance of the different control algorithms in terms of Root Mean Square Errors, as it is shown in Table 1. As expected, the Adaptive DOB performs better than both the Conventional controller and the Normal DOB.

Table 1 Simulation results (RMSE)

4. Conclusion

We introduce a control algorithm for tracked vehicles that ensures path-tracking capabilities while moving in presence of slip phenomena, due to either rough terrain and/or ground inclination. The algorithm relies on the combination between a DOB and a parametric kinematic model in order to compensate slip phenomena. An adaptive control law allows to modify the parameter of the model in order to let the DOB robustly compensate slipping. The performance of the proposed controller is verified in simulation environment. A comparison between the proposed controller and a more conventional one is also discussed.

References

• [1]N. Noguchi and O. C. Barawid Jr., “Robot farming system using multiple robot tractors in Japan agriculture”, In 18th IFAC world congress, 2011.
• [2]S. Blackmore, “New concepts in agricultural automation”, In HGCA conference, 2009.
• [3]D. Ball, P. Ross, A. English, P. Milani, D. Richards, A. Bate, B. Upcraft, G. Wyeth and P. Corke, “Farm workers of the future”, In IEEE Robotics & Automation magazine, 2017.
• [4]J. Pentzer, S. Brennan and K. Reichard, “Model-based Prediction of Skid-steer Robot Kinematics Using Online Estimation of Track Instantaneous Centers of Rotation”, In Journal of Field Robotics, 2014.
• [5]C. Wen-Hua, Y. Jun, G. Lei and L. Shihua, “Disturbance-observer-based control and related methods – An overview,” In IEEE Transl. Industrial electronics., vol. 63, Feb. 2016, pp. 1083–1095
• [6]S. Hyungbo, P. Gyunghoon, J. Youngjun, B. Juhoon and J. Nam Hoon, “Yet another tutorial of disturbance observer: robust stabilization and recovery of nominal performance”, In Control theory and technology. South China University of technology and academy of mathematics and systems science, vol. 14, Aug., 2016, pp. 237-249
• [7]R. Gonzàlez, R. Rodoriguez and J. Guzmàn, “Autonomous Tracked Robots in Planar Off-Road Conditions”, Springer, 2014.
• [8]Y. Kanayama, Y. Kimura, F. Miyazaki and T. Noguchi, “A Stable Tracking Control method for an autonomous mobile robot”, In Proceedings of IEEE International Conference on Robotics and Automation, 1990.
• [9]T. M. Dar and R. G. Longoria, “Estimating traction coefficients of friction for small-scale robotic tracked vehicles”, In Proceedings of the ASME 2010 Dynamics Systems and Control Conference, 2010
• [10]B. M. Nguyen, H. Fujimoto, Y. Hori, “Yaw angle control for autonomous vehicle using Kalman filter based disturbance observer”, In SAEJ. EVTeC and APE Japan, 2014.
• [11]J.-J. E. Slotine and W. Li, “Applied Nonlinear Control”, Prentice Hall, 1991.
• [12]F. Pourboghrat and M. P. Karlsson, “Adaptive control of dynamic mobile robots with nonholonomic constraints”, In Computers and Electrical Engineering 28, 2002.
• [13]Boost-up your research work without wasting time and money, retrieved January 25, 2019 from http://www.dronyx.com/xbot-tracked-mobile-robot/.
• [14]V-rep virtual robot experimentation platform, retrieved January 25, 2019 from http://www.coppeliarobotics.com/.
• [15]Achieve true-to-life simulation, retrieved January 25, 2019 from
  https://www.cm-labs.com/vortex-studio/features/physics-based-mechanical-dynamics-engine/.
• [16]T. Hiramatsu, S. Morita, M. Pencelli, M. Niccolini, M. Ragaglia and A. Argiolas, “Path-Tracking Controller for Tracked Mobile Robot on Rough Terrain”, In International Conference on Field and Service Robotics, 2019
• [17]S. Morita, T. Hiramatsu, M. Niccolini, A. Argiolas, M. Ragaglia, “Kinematic track modelling for fast multiple body dynamics simulation of tracked vehicle robot”, In The 24th International Conference on Methods and Models in Automation and Robotics, 2018