ヤンマーホールディングス株式会社 技術本部
中央研究所 基盤技術研究センター
ヤンマーテクニカルレビュー
モジュラーデザインを想定したComponent TPA手法の研究
~オフロード車両を用いた実験的アプローチによる精度検証~
Abstract
The Yanmar Group is promoting the diversification of its prime mover, including electrification and carbon-neutral fuels. In this regard, we are promoting the application of Component TPA (hereinafter referred to as C-TPA) to completed vehicles, with a view to modular design for off-road vehicles, including those for construction and agricultural use. In this study, we investigate the effects of nonlinearity of acceleration in a forced vibration system generated by a prime mover and the number of conditions when identifying blocked forces using the inverse matrix method, focusing on off-road vehicles.
1. はじめに
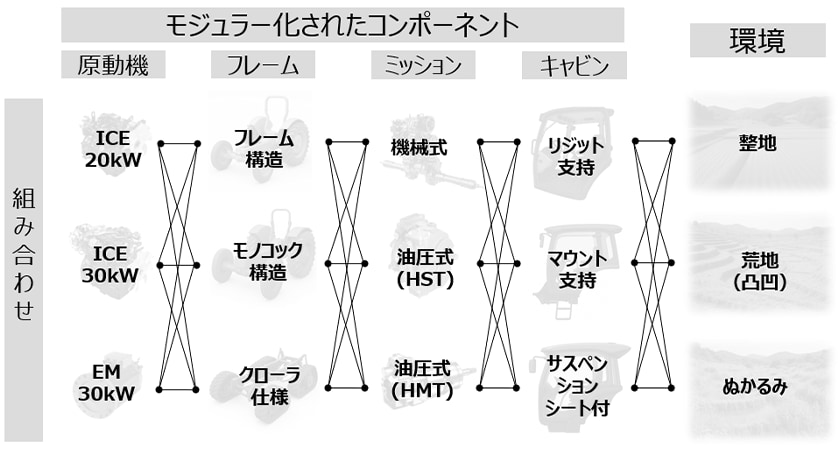
建設機械や農業機械に代表されるオフロード車両は、図1に例示するとおり、原動機・フレーム・ミッション・キャビンなど仕様のバリエーションが多い。さらにアタッチメントからの外力や圃場路面の凹凸など、作業条件も多岐にわたる。これらの組み合わせは膨大であり、設計および評価工数の増大を招いている。このような背景から、当社では車両開発の効率化を目的として、オフロード車両へのモジュラーデザインを推進中である。
モジュラーデザインを効果的に進める技術の一つとして、近年自動車業界で関心が高まっているコンポーネントTPA(以下C-TPA)手法がある(1)(2)。C-TPAは、各コンポーネントの振動伝達特性を個別に取得し、それらを仮想的に組み合わせることで、実機を組み立てずにシステム全体の振動・騒音を予測・評価できる点に特徴がある。この手法を適用することで、コンポーネント構成の変更に対しても実機試作を行うことなく予測・評価できるため、設計段階での検討自由度が高まり、試作回数の削減や開発効率の向上が期待される。
一方で、C-TPAは自動車業界も含め完成車両への適用事例がなく、誤差低減をはじめとする技術的課題がある(3)(4)。特に開発での実用化に向け、①線形系を前提とした手法の適用、②逆行列における条件数の適切な調整(4)が重要な論点である。本研究では、オフロード車両への振動レベル推定を対象として、これら2点の影響調査および考察を報告する。
2. C-TPAでの振動レベルの推定スキーム
C-TPAでは、起振源となるコンポーネント(以下アクティブコンポーネント)と振動伝達経路となるコンポーネント(以下パッシブコンポーネント)からそれぞれ固有の振動特性を線形結合してシステム応答を求める。また、完成車の実稼働中に直接計測できる加振力(以下コンタクトフォース:C.F.)はパッシブコンポーネントの振動特性に依存するためC-TPAへの活用には制約がある。そのため、パッシブコンポーネントに依存しない固有の加振力であるブロックドフォース(以下B.F.)を求めるB.F.法(5)(6)を用いたC-TPAを進める。
応答点の振動レベルVLは、アクティブ/パッシブ、各コンポーネント固有の振動特性から図2のような(i)B.F.同定、(ii)C.F.同定、(iii)応答点推定の三段階のスキームで推定できる。ここで、BFr、BFiはそれぞれ異なるパッシブコンポーネントで同定したB.F.で、VLCTPA、VLはそれぞれ本スキームで推定した振動レベルと実験での振動レベルである。
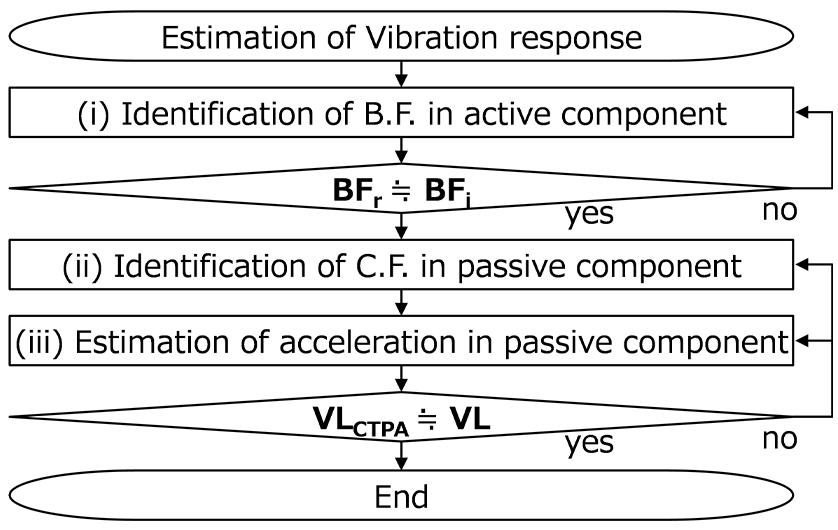
図3は、強制振動系を模式的に示しており、原動機を抽象するアクティブコンポーネントと車体を抽象するパッシブコンポーネントを定義している。ここで、図中の数字1~5は、それぞれ表1に示す起振力の原点、加振力の力点、加振力の作用点、振動の参照点および応答点を示す。
図2のプロセス(i)では、図3のアクティブコンポーネントでの起振力(ポイント1)に起因するB.F.の力点(ポイント2)とパッシブコンポーネントでの参照点(ポイント4)間のアクセレランスH42および参照点(ポイント4)の実稼働時の加速度a4から次式のとおりB.F.を同定する。
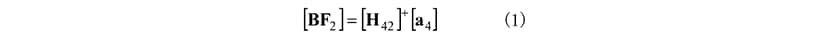
ここで、BF2は力点(ポイント2)でのB.F.を示す。
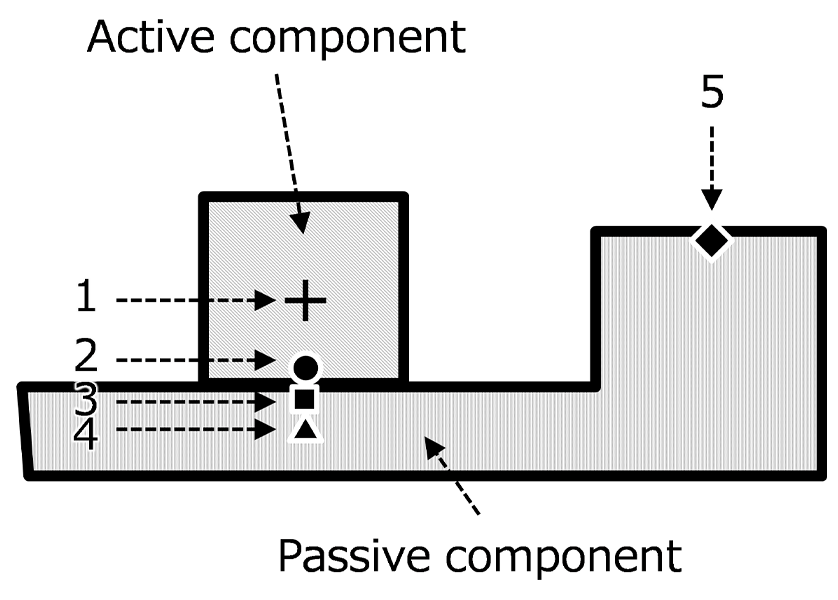
Table 1 Definition of each point in a forced vibration system
| Symbol Number | Symbol | Definition |
|---|---|---|
| 1 | + | Vibration source |
| 2 | ● | Effort point |
| 3 | ■ | Load point |
| 4 | ▲ | Reference point |
| 5 | ◆ | Response point |
図2のプロセス(ii)では、図3のアクティブコンポーネントの力点(ポイント2)のB.F.からパッシブコンポーネント(ポイント3)に作用するC.F.を同定する。次式のとおり、C.F.はアクティブ/パッシブ、各コンポーネントのアクセレランスH22およびH33とアクティブ-パッシブコンポーネント間のマウント剛性Kから伝達関数合成法(7)を応用して次式のように求められる。
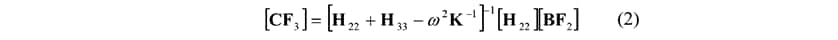
ここで、CF3はパッシブコンポーネントの作用点(ポイント3)でのC.F. 、ωは角速度である。
図2のプロセス(iii)では、図3のパッシブコンポーネントの作用点(ポイント3)でのC.F.と作用点-応答点間のアクセレランスH53から応答点(ポイント5)の加速度a5を次式のとおり推定する。
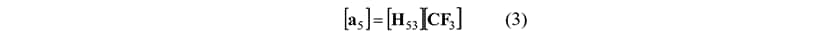
また、推定した応答点の加速度a5にISO 2631(8)で規定されている全身振動の感覚に基づく周波数荷重を施し、振動レベルVLCTPAを求める。
3. 研究対象
3.1. オフロード車両
研究対象のオフロード車両は、図4および表2の定格出力66 kW、排気量3.1 Lの直噴ディーゼル機関を搭載した車重3.5 tの農業用トラクタである。一般に農業用トラクタには原動機を防振支持する車両と剛結合する車両の二種あるが、本車両は防振支持である。

Table 2 Vehicle information
| Vehicle | Type | Agricultural Tractor |
|---|---|---|
| Length | 4.1 [m] | |
| Width | 1.8 [m] | |
| Height | 2.8 [m] | |
| Weight | 3.5 [t] | |
| Prime mover | Type | 4-cycle 4-cylinder diesel |
| Displacement | 3.1 [L] | |
| Rated output | 66 [kW] | |
| Rated speed | 2530 [min-1] |
3.2. 運転モードおよび振動レベルの評価
農業用トラクタは、高負荷かつ一定車速での作業が典型であり、原動機の回転速度は定格回転で、車速はトランスミッションで調節されることが多い。本研究では原動機に起因する強制振動系に着眼するため、運転モードを表2に示しているディーゼル機関の定格回転速度でのアイドリング運転(以下ハイアイドル運転)とする。また、振動レベルVLは第2章に記述のとおり、ISO 2631に規定されている周波数荷重が課されるため、表2に示している強制加振系ではディーゼル機関の燃焼に起因する1次周波数成分ffreq = 84 Hzの振動が支配的で、高次周波数成分は微小となる。
3.3. 強制振動系
対象車両での強制振動系は、図5のようにディーゼル機関を抽象するアクティブコンポーネントとフレーム構造の車体を抽象するパッシブコンポーネントで定義できる。パッシブコンポーネントへの作用点(ポイント3)からC.F.が入力され、フレーム構造を介して運転席下へ振動が伝達される。第2章で示した式(1)~(3)の各変数は、図5に示す振動伝達経路上の位置で表3に示す点数で求めている。なお、ディーゼル機関の軸動力はドライブシャフトを介してトランスミッションに伝達されるが、3.2.節のとおり運転モードはクラッチで動力遮断されているハイアイドル運転につき、ドライブシャフト経由の振動伝達経路は無視できる。
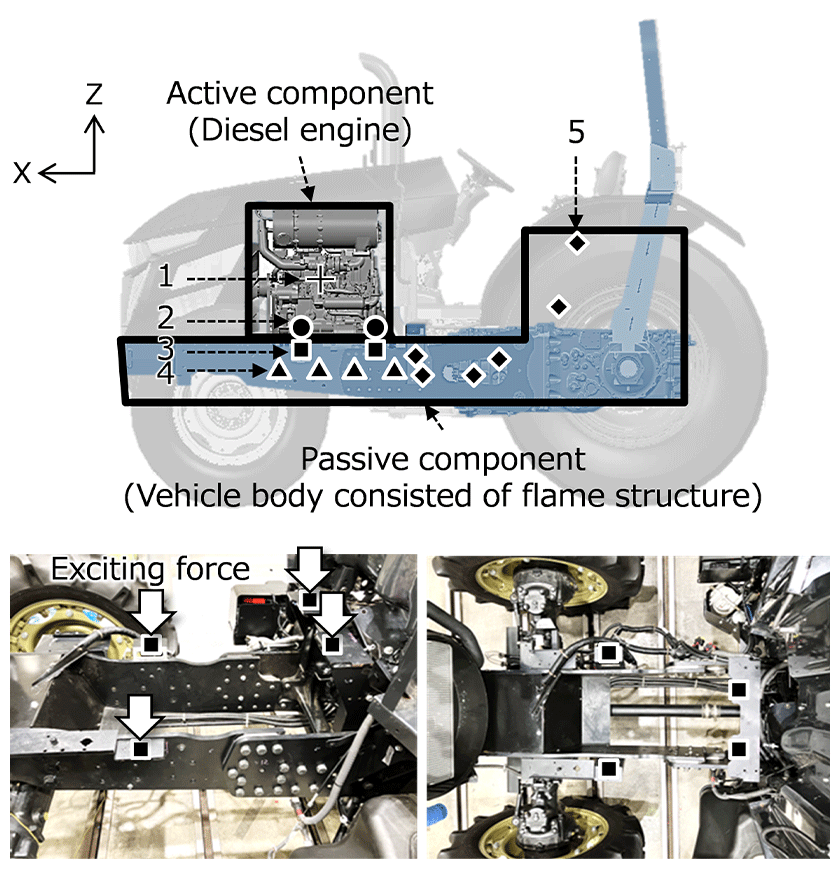
Table 3 Measurement points for C-TPA on the off-road vehicle
| Symbol Number | Symbol | Definition | Number of measurement points |
|---|---|---|---|
| 2 | ● | Effort points | 4 |
| 3 | ■ | Load points | 4 |
| 4 | ▲ | Reference points | 8 |
| 5 | ◆ | Response points | 6 |
4. オフロード車両へのC-TPAの適用検討
4.1. 強制振動系の線形性
線形系を前提とするC-TPAをオフロード車両の強制振動系に適用するにあたり、打撃加振力Fと振動応答aの線形性を調査する。図6は、打撃加振実験での力点のアクセレランスH22の一成分H22と作用点-応答点間のアクセレランスH53の一成分H53を代表に示しているが、アクセレランスH22は打撃加振力について一定で、ディーゼル機関からなるアクティブコンポーネントには線形性が認められる。一方で、アクセレランスH53には打撃加振力Fの強弱でレベル差があり、車体からなるパッシブコンポーネントには非線形域が確認できる。フレーム構造のオフロード車両では、図5の左下図のようにフレーム間の結合はボルト締結で、ボルト軸力が作用する局所以外は接触拘束である。したがって、低入力ではズレやガタの影響が小で出力応答が相対的に高く、高入力ではズレやガタの影響が大で出力応答が相対的に低くなると考察できる。ただ、非線形性は打撃加振力Fが比較的弱い領域(F < 4 N)に限定的であり、車両実稼働時に相当する領域の線形性/非線形性を調査している。図7(a)は打撃加振実験での打撃加振力Fと応答点の加速度a5の関係、図7(b)は車両実稼働時の応答点の加速度a5である。実稼働時の加速度応答に対応する打撃加振実験での加振力は直接計測できないため、次のプロセスで同定する。
Step1. 実稼働時のffreq = 84 Hzの加速度(図7(b)a5=130~135 dB)を計測。
Step2. 様々な打撃加振力でのffreq = 84 Hzの加速度を計測(図7(a))。
Step3. 図7(b)のa5=130~135 dB相当の打撃加振力(図7(a))を同定。
本プロセスで同定した実稼働時の加速度応答に対応する打撃加振実験の加振力Fは図7のとおり7 N程度で、車両実稼働時の強制振動系は線形域にあると認められる。したがって、本強制振動系にC-TPAが適用できると判断でき、非線形要素があるフレーム構造からなるオフロード車両でのC-TPAでは、図2に示したスキームの前段に系の線形性確認のプロセスを加えるべきと考える。
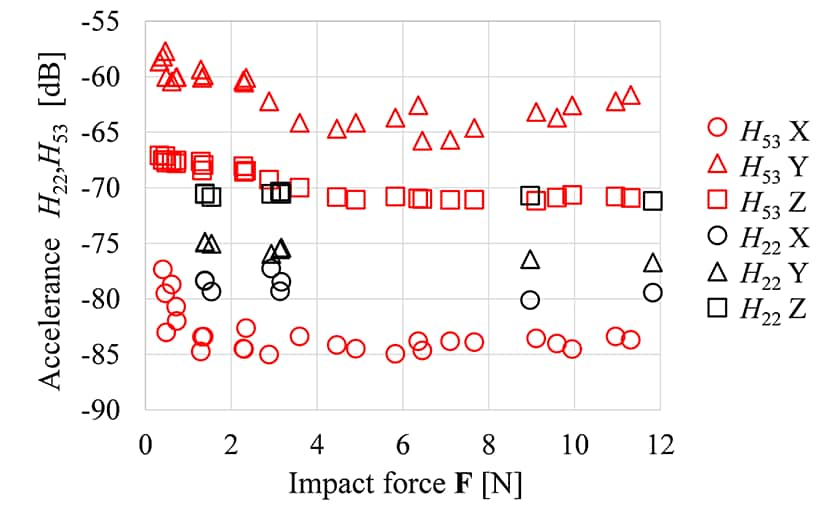
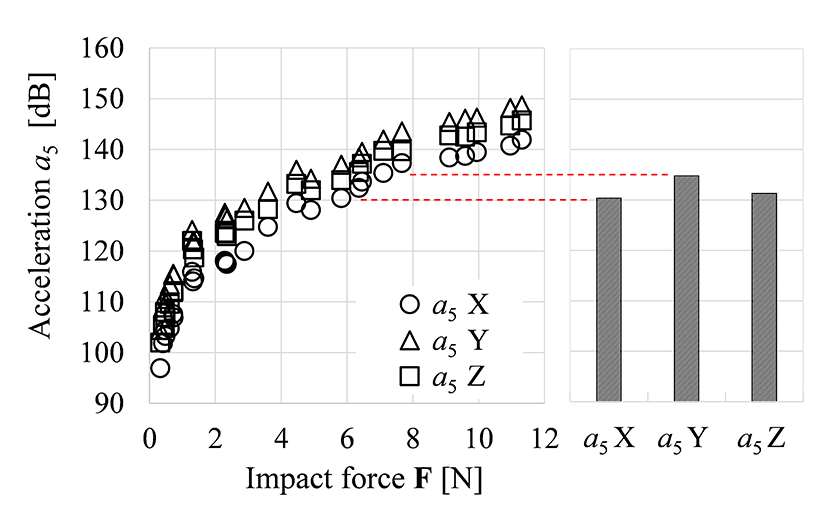
Fig.7 Acceleration of 84 Hz at response point 5
4.2. 逆行列法での誤差鋭敏性
式(1)の逆行列演算を介して求められるB.F.の誤差鋭敏性を考察する。本研究では、入力および出力信号への誤差の要因が未知のなかで進められるモジュラーデザインを想定し、条件数k(9)の調整による誤差の鋭敏性低減化のアプローチを検討する。図8は、H42の逆行列演算時の条件数kに応じた応答点の加速度a5 を示す。条件数kは101のオーダーで比較的に誤差の拡大率は小さいが、条件数kによっては応答点の加速度に数十dBの差異が発現しており調整の余地がある。条件数kの調整では誤差の影響が比較的大きいと考えられる最小特異値から順に無視していくが、図8のように条件数k < 10では応答点の加速度a5は急峻に低減している。条件数kは最大特異値と最小特異値の比、すなわち応答に対する伝達経路の影響と計測誤差の影響の比と理解でき、条件数kの数学的解釈から過剰な調整は寄与が高い伝達経路の無視をもたらすと理解できる。したがって、B.F.の誤差鋭敏性を下げる条件数kの調整では、加速度応答の変化δa5/δkが比較的小さい条件数kの選択が合理的である。
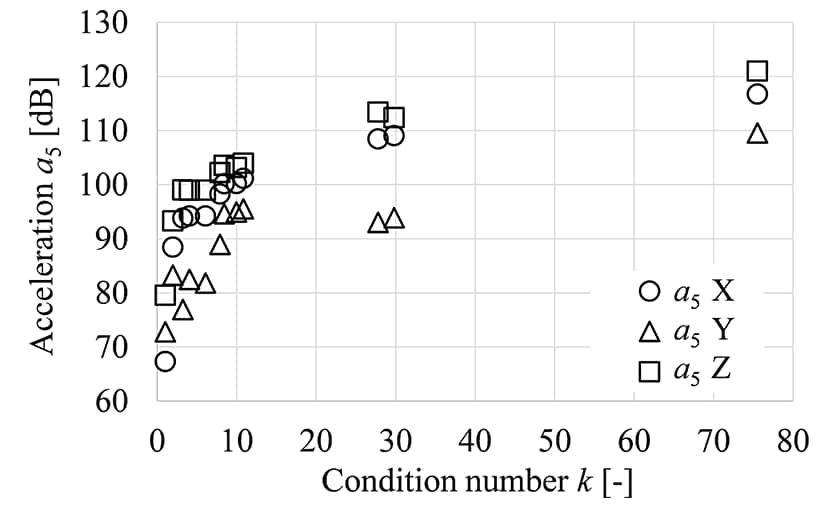
(ffreq = 84 Hz, near the seat in a5)
4.3. 自由端条件でのアクセレランス計測
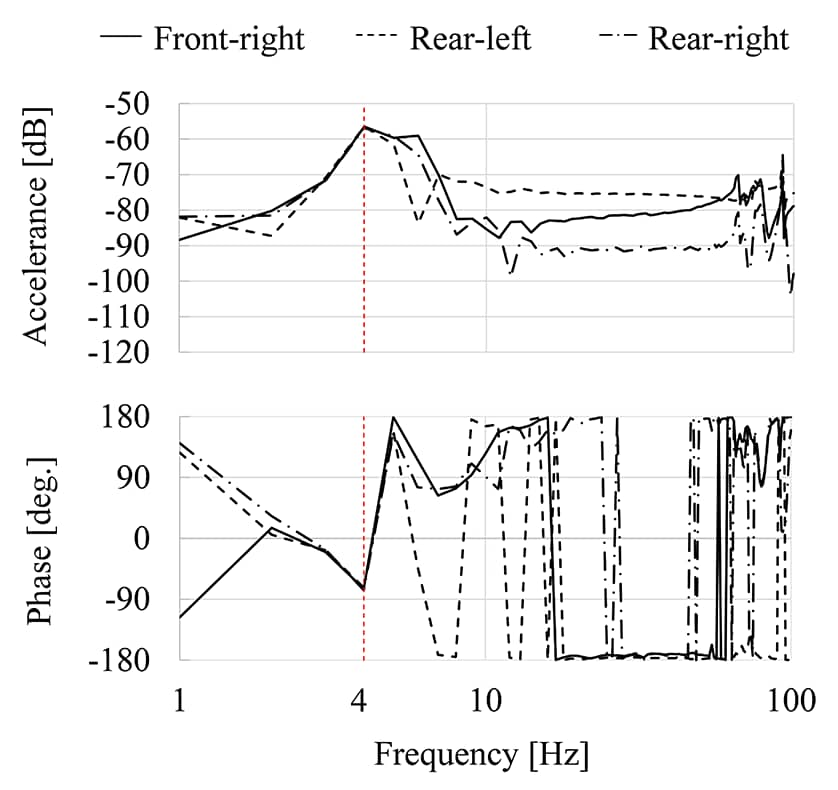
式(2)のアクティブコンポーネント固有のアクセレランスH22は、自由端条件での打撃加振実験で求められ、本研究では自由端条件を図9のようなエアマウント支持で近似する。図10は、表3に示している力点(ポイント2)での打撃加振点(車両左前)を除く3点(車両右前、左後、右後)のアクセレランスH22で、振幅峰および位相の回りが同一であることから4 Hz付近に剛体モードが認められる。また、本剛体モードは着眼しているディーゼル機関の燃焼1次成分ffreq = 84 Hzと乖離していることからも剛体モードと判断でき、アクティブコンポーネント固有のアクセレランスH22が適切に得られていると判断できる。

5. オフロード車両での振動レベル推定
5.1. B.F.の同定
B.F.は、パッシブコンポーネントの如何を問わず不変の起振力であるため、B.F.同定の確からしさは異なるパッシブコンポーネントで同定したそれぞれのB.F.の一致性で検証する。図11は、ディーゼル機関を車両に防振支持した際のBFiを横軸、剛結合で支持した際のBFrを縦軸にとり、複数の打撃加振実験での加振力(F = 2 N, F = 7 N)および条件数(k = 10, k = 78)で同定したB.F.である。パッシブコンポーネントの非線形域にあたる比較的弱い打撃加振力(F = 2 N)で条件数kが比較的に高い(k = 78)場合は、BFiとBFrの乖離は15 dB程度と比較的大きく、4.1.節で提案している線形域の確認プロセスや4.2.節の誤差の鋭敏性低減化の重要性がわかる。これらを考慮して同定したB.F.(F = 7 N、k = 10)は、BFiとBFrの一致性が高く、パッシブコンポーネントに依存しないアクティブコンポーネントの固有特性が同定できている。
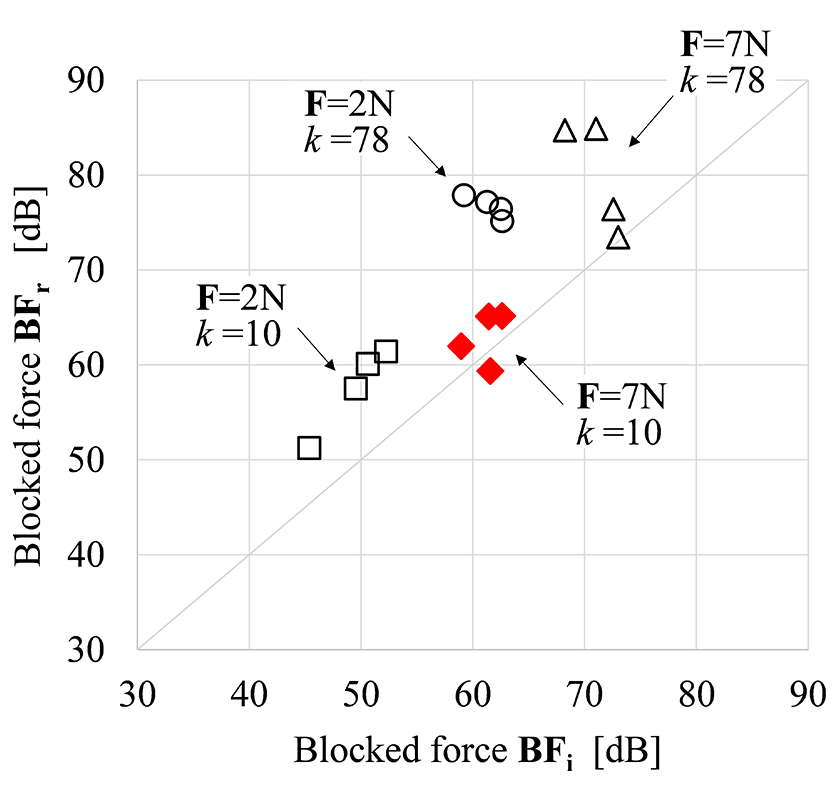
condition number(ffreq = 84 Hz)
5.2. C.F.の同定
C.F.はB.F.を式(2)に入力して同定するが、式(2)のマウント剛性Kは、防振ゴムの動的特性をJIS K6385 防振ゴム -試験方法-に準じて求めている。図12は前節と同様に複数の打撃加振実験での加振力(F = 2 N, F = 7 N)および条件数(k = 10, k = 78)で同定したB.F.を介して求めたC.F.である。打撃加振実験での加振力Fおよび条件数kに応じて同定したC.F.に差異が生じており、これらを適切に選択することの重要性がわかる。
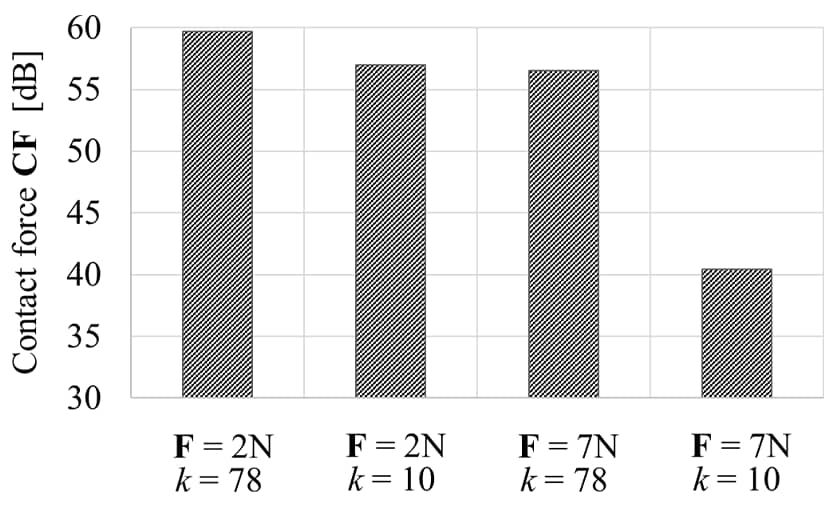
condition number(ffreq = 84 Hz)
5.3. 振動応答および振動レベルの推定
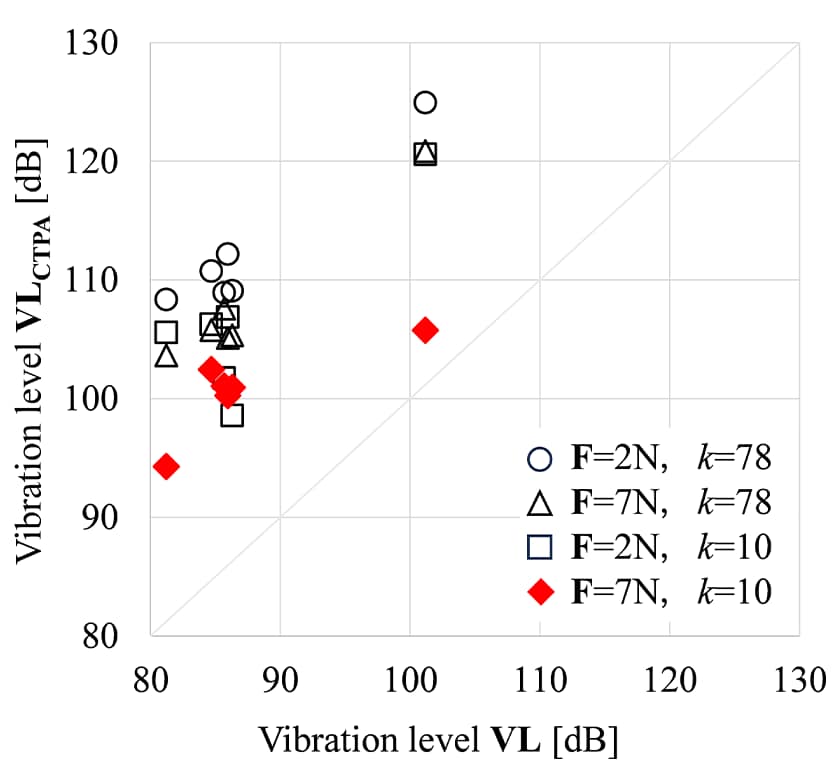
応答点の加速度a5および振動レベルVLCTPAは、式(3)のとおりC.F.とパッシブコンポーネントの作用点-応答点間のアクセレランスH53から求める。図13はC-TPAによって推定した振動レベルVLCTPAと車両実稼働時の振動レベルVLの対比を示しており、ここでも複数の打撃加振実験での加振力(F = 2 N, F = 7 N)および条件数(k = 10、k = 78)で比較する。第4章の考察を踏まえた比較的高い加振力(F = 7 N)および調整済み条件数(k = 10)での振動レベルVLCTPAは、他と比較して車両実稼働時の振動レベルVLに近く、線形性の確認プロセスや誤差鋭敏性の調整の重要性が示唆されている。
6. おわりに
車両開発の効率化を目的としたモジュラーデザインの推進に向けて、フレーム構造からなるオフロード車両の完成車を対象に、内燃機関に起因する強制振動系の振動レベル推定にC-TPAを適用した。さらに、アクセレランスの非線形性や逆行列法における条件数kの影響について調査および考察した。本調査および考察から、オフロード車両にC-TPAを適用する際の技術的課題に対し、以下の知見を得た。
① 打撃加振実験における加振力Fと応答の線形性について、弱い加振力領域では非線形性が生じ、ある程度強い加振力領域で線形性が維持されることを明らかにした。これにより、C-TPAの適用に際しては、線形性の確認および適切な加振力設定が不可欠であることが示された。
② 逆行列演算における誤差鋭敏性について、条件数kの大小によって振動応答が数十dB変動し得ることを明確にし、誤差を最小化するための条件数調整手法を提示した。
今後、C-TPAによる振動レベル推定の更なる信頼性向上に向けて、着目周波数帯の振動モードを十分に捉える計測位置・点数の最適化や、動質量行列法をはじめとした逆行列演算過程における誤差低減が課題(3)(4)であると考えている。 これらの知見と今後の課題を踏まえ、当社のモジュラーデザインへのC-TPA適用を一層推進し、オフロード車両開発の効率化に貢献していく。
参考文献
- (1)D. de Klerk, D.J. Rixen:Component transfer path analysis method with compensation for test bench dynamics, Mechanical Systems and Signal Processing, Vol.24, No.6, pp.1693-1710(2010)
- (2)M. V. van der Seijs, D. de Klerk, D. J. Rixen:General framework for transfer path analysis : History, theory and classification of techniques, Mechanical Systems and Signal Processing, Vol.68-69, pp.217-244(2016)
- (3)小林樹幸, 吉村卓也:逆行列を用いた入力同定の分散評価, 日本機械学会集(C編), Vol.77, No.776, pp.162-175(2011)
- (4)小林樹幸, 吉村卓也:動質量行列を用いた入力同定法の提案, 日本機械学会集(C編), Vol.75, No.753, pp.278-285(2009)
- (5)A.S. Elliott, A.T. Moorhouse:Characterisation of structure borne sound sources from measurement in-situ, Acoustics’08 Paris, pp.1477-1482(2008)
- (6)A.T. Moorhouse, A.S. Elliott, T.A. Evans:In situ measurement of the blocked force of structure-borne sound sources, Journal of Sound and Vibration, Vol.325, No.4-5, pp.679-685(2009)
- (7)長松昭男, 大熊政明:部分構造合成法, 培風館, p.94(1991)
- (8)ISO 2631-1:1997 Mechanical vibration and shock - Evaluation of human exposure to whole-body vibration -Part 1: General requirements(1997)
- (9)伊理正夫, 児玉慎三, 須田信英:特異値分解とそのシステム制御への応用, 計測と制御, 21巻, 8号, pp.763-772(1982)
著者
